รายชื่อสมาชิกกลุ่ม

1. ภัทราพร ยั่งยืน ม.6/2 เลขที่ 41

2. ภรณ์ประภา ปานประภากร ม.6/2 เลขที่ 42

3. ชลธิชา ผาสุพรรณ์ ม.6/2 เลขที่ 44

4. ชนิกานต์ กิติเวชโภคาวัฒน์ ม.6/2 เลขที่ 46

5. คนิดาริน ปานยิ้ม ม.6/2 เลขที่ 47

โจทย์ เรื่อง ไฟฟ้ากระแสสลับ

1.

2.

3.

4.

5.

เฉลย

ไฟฟ้ากระแสสลับ

ไฟฟ้ากระแสสลับ

ไฟฟ้า กระแสสลับหมายถึงกระแสไฟฟ้าที่มีการสลับสับเปลี่ยนขั้วอยู่ตลอดเวลาอย่าง สม่ำเสมอ ทิศทางการไหลของกระแสไฟฟ้า ก็จะเปลี่ยนสลับไปมาจากบวก-ลบและจากลบ-บวก อยู่ตลอดเวลา ซึ่งไฟฟ้ากระแสสลับเป็นไฟฟ้าที่ใช้กันตามบ้านเรือนและโรงงาน อุตสาหกรรมทั่วไปเมื่อเรานำไฟฟ้ากระแสสลับมาเขียนเป็นกราฟความสัมพันธ์ ระหว่างแรงดันไฟฟ้ากับมุมที่เปลี่ยนไปเมื่อเวลาผ่านไปในขณะที่เกิดการไหล ของกระแสไฟฟ้าจะได้ความสัมพันธ์ของกราฟเป็นเส้นโค้งสลับขึ้นลงไปมาซึ่งหมาย ถึงเมื่อเวลาผ่านไปแรงดันไฟฟ้าจะสลับการไหลตลอดเวลา การไหลของกระแสสลับกลับไป กลับมาครบ1รอบ เรียกว่า 1 ไซเคิล (cycle) หรือ 1 รูปคลื่นและจำนวนรูปคลื่น ทั้งหมดในเวลาที่ผ่านไป 1 วินาที เรียกว่า ความถี่(frequency) ซึ่งความถี่ ไฟฟ้ามีหน่วยวัดเป็นรอบต่อวินาทีหรือรูปคลื่นต่อวินาทีหรือไซเคิลต่อวินาที มีหน่วยย่อเป็น"เฮิรตซ์"(Hertz)สำหรับความถี่ไฟฟ้าในประเทศ ไทยเท่ากับ 50 เฮิรตซ์

การกำเนิดไฟฟ้ากระแสสลับ

ค่าของแรงดันไฟฟ้ากระแสสลับจะเกิดขึ้นมากหรือน้อยนั้น ขึ้นอยู่กับตำแหน่งของขดลวดตัวนำขณะหมุนตัดกับเส้นแรงแม่เหล็กในสนามแม่ เหล็กนั้น ถ้าทิศทางการเคลื่อนที่ของขดลวดตัวนำตั้งฉากกับเส้นแรงแม่เหล็ก แรงดันไฟฟ้าที่เกิดขึ้นจะมีค่าสูงสุดและจะมีค่าน้อยลง เมื่อทิศทางการเคลื่อนที่ของขดลวดตัวนำตัดกับเส้นแรงแม่เหล็กในมุมน้อยกว่า 90๐ และจะมีค่าเป็นศูนย์เมื่อขดลวดตัวนำวางขนานกับเส้นแรงแม่เหล็ก

จะเห็นว่าใน 1 วัฎจักรของการหมุนขดลวดตัวนำ คือ หมุนไป 360๐ ทางกลน้ำจะเกิดรูปคลื่นไซน์ 1 ลูกคลื่น หรือ 1 วัฎจักร ถ้าขดลวดตัวนำนี้หมุนด้วยความเร็วคงที่และสภาพของเส้นแรงแม่เหล็กมีความหนา แน่นเท่ากันตลอด รอบพื้นที่ของการตัดแรงดันไฟฟ้าสลับรูปคลื่นไซน์ที่จะมีค่าคงที่และถ้ามีการ หมุนของขดลวดต่อเนื่องตลอดไป จะทำให้เกิดจำนวนรอบของแรงดันไฟฟ้าเหนี่ยวนำต่อเนื่องกันไป นั่นคือการเกิดแรงดันไฟฟ้ากระแสสลับ

ความถี่และคาบเวลาของไฟฟ้ากระแสสลับ

ความถี่ของกระแสสลับ (Frequency ตัวย่อ f) หมายถึง จำนวนวัฏจักรของการเกิดรูปคลื่นไซน์ต่อเวลา 1 วินาที

ถ้าเกิดรูปคลื่นไซน์ 2 วัฏจักรต่อเวลา 1 วินาที ก็แสดงว่าไฟฟ้ากระแสสลับที่เกิดขึ้นมีความถี่ 2 วัฏจักรต่อเวลา 1 วินาที หรือเรียกแทนในหน่วยเฮิรตซ์ (Hz) หรือความถี่ไฟฟ้ากระแสสลับ 50 เฮิรตซ์ ก็คือการเกิดรูปคลื่นไซน์จำนวน 50 วัฏจักรต่อเวลา 1 วินาที และจากรูป 4.2 รูปคลื่นไซน์นี้มีความถี่เท่ากับ 1 เฮิรตซ์ เป็นต้น

ความถี่และคาบเวลาของไฟฟ้ากระแสสลับ

ค่าต่างๆ ที่สำคัญของรูปคลื่นไซน์ นอกจากความถี่และคาบเวลานั้นมีอีก 4 ค่า คือ ค่าสูงสุด(Maximum) ค่ายอดถึงยอด(Peak-to-Peak) ค่าเฉลี่ย(Average) และค่าใช้งาน(Effective)

มุมและความเร็วเชิงมุม

มุมใน 1 วัฏจักรการกำเนิดรูปคลื่นไซน์อย่างสมบูรณ์นั้น ประกอบด้วยจำนวนมุมของการวัดในหน่วยองศารวม 360 องศา แต่ใน 1 รอบวงกลมนั้นเราแบ่งออกเป็น 4 ส่วนหรือ 4 ควอแดนท์ แต่ละส่วนมีค่ามุมส่วนละ 90 องศา ตามทิศทางของลูกศร ซึ่งแต่ละ90 องศา ก็คือความยาวในแกนนอนของกราฟรูปคลื่นไซน์โดยมีแกนตั้งเป็นแกนบอกขนาด ซึ่งอาจเป็นขนาดของกระแสหรือแรงดันของไฟสลับ

ความเร็วเชิงมุม(Angular Velocity) หรือ (โอเมก้า) หมายถึง จำนวนมุม(ในหน่วยเรเดียน) ที่รัศมีของวงกลมหมุนผ่านไปต่อ 1 วินาที

ค่าสูงสุดกับค่ามิเตอร์

เมื่อนำตัวต้านทานต่อเข้ากับเครื่อง กำเนิดไฟฟ้ากระแสสลับจะมีกระแส สลับผ่านตัวต้านทานและมีความต่างศักย์ไฟฟ้าระหว่าง ปลายทั้งสองข้าง ของตัวตานทาน

ค่าของปริมาณทั้งสองเปลี่ยนแปลงตามเวลาดังกราฟ

เนื่องจากไฟฟ้ากระแสสลับจะมีค่าเปลี่ยน แปลงตลอดเวลา (t) ดังนั้นในการ เขียนค่าความสัมพันธ์ต่าง ๆ เช่น EMF, ความต่างศักย์ หรือกระแสไฟฟ้าจะอยู่ในความสัมพันธ์ของฟังก์ชัน sine ซึ่งจะเขียนได้ดังนี้

ความสัมพันธ์ระหว่างค่าสูง สุดกับค่ามิเตอร์ หรือ rms

เมื่อป้อนกระแส I = I_m sinωt กับความต้านทาน R

กำลังที่เสียไปที่ตัวต้านทาน R เขียนได้เป็น P = I²R

P = [(I_m²)sin²ωt] R

P = [(I_m²)R] sin²ωt

ดังนั้น จะได้ว่า [(I_m²)R] sin²ωt = I²R

เนื่องจากเทอม [(I_m²)R] sin²ωt จะมีค่าเป็นบวกตลอดเวลา และมีค่าไม่คงที่

ถ้าเราหาค่าเฉลี่ยใน 1 คาบ จะพบว่าค่าเฉลี่ยของ sin²ωt เท่ากับ 1/2

P = I_m² R (1/2)

ถ้าป้อนกระแสคงที่ผ่านตัวต้านทาน R ให้ได้กำลังเท่ากับกำลังเฉลี่ย จะได้ว่า

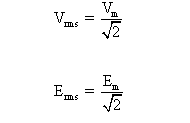
V = V_m sin ωt เมื่อ ω = 2Πf
และ I = I_m sin ωt
เมื่อ V_m = ความต่างศักย์สูงสุด
มีหน่วยเป็น โวลต์ (V) I_m = กระแสไฟฟ้าสูงสุด มีหน่วยเป็น แอมแปร์ (A)
จากสมการเราได้ว่า V หรือ I คือ ค่ายังผล หรือค่า มิเตอร์

หรือค่ารากที่สองของค่าเฉลี่ยของกำลังสองของ ความต่างศักย์และกระแสไฟฟ้า
ใช้ VRMS และ IRMS ซึ่งเป็นค่าที่วัดได้จากเครื่องวัดกระแสสลับและใช้ค่านี้ในการคำนวณ โดยมีความสัมพันธ์ดังนี้
Vm = √2 Vrms
Im = √2 Irms
โดยทั่วไปเครื่องวัดปริมาณต่าง ๆ ของไฟฟ้ากระแสสลับ เช่น ความต่างศักย์ไฟฟ้า กระแสไฟฟ้า จะออกแบบให้วัดค่า rms
เช่น ไฟฟ้ากระแสสลับที่ใช้ตามบ้านเรือนที่เขียนว่า 220 V ค่านี้หมายถึง ค่ายังผล หรือ rms ซึ่งถ้าจะหาค่าสูงสุดก็จะได้เท่ากับ 311V

คุณสมบัติของไฟฟ้ากระแสสลับ

1. สามารถส่งไปในที่ไกล ๆ ได้ดี กำลังไม่ตก
2. สามารถแปลงแรงดันให้สูงขึ้นหรือต่ำลงได้ตามต้องการโดยการใช้หม้อแปลง (Transformer)


เฟส และมุมเฟส

เฟส (Phase)

เมื่อเขียนกราฟระหว่าง sinωt กับ t จะเรียกตำแหน่งต่าง ๆ บนเส้นกราฟว่า เฟส(phase)
โดยที่ ที่เวลา t = 0 ค่า sinωt มีค่าเป็นศูนย์ จะมีเฟสเท่ากับ ศูนย์
และเมื่อเวลาผ่านไป sinωt มีค่าสูงสุดเป็นครั้งแรก (จุด A) จะมีเฟส เท่ากับ π/2


เฟสนำและเฟสตาม

เมื่อเทียบกับ sinωt แล้วจะมีเฟสตามอยู่ π/2 เรเดียน

เมื่อเทียบกับ sinωt แล้วจะมีเฟสนำอยู่ π/2 เรเดียน

ไฟฟ้ากระแสสลับ - ขดลวดเหนี่ยวนำ

ส่วนประกอบของวงจรไฟฟ้ากระแสสลับ ได้แก่ ตัวต้านทาน (R) ตัวเก็บประจุ (C) และขดลวดเหนี่ยวนำ (L)

1.วงจร ตัวต้านทาน (R) เมื่ออยู่ในวงจรไฟฟ้ากระแสสลับที่มีกระแสไฟฟ้า I และมีความต่างศักย์ Vจะมีสมบัติเหมือนกันและคำนวณหาความต้านทาน (R)โดยใช้กฎของโอห์ม

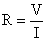จากกฎของโอห์มและกราฟจะได้ว่า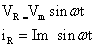

จึงได้ว่า “ กระแสสลับที่ผ่านตัวต้านทานและความต่างศักย์ไฟฟ้าระหว่าง ปลายของตัวต้านทานมีเฟสตรงกัน”

2. วงจรตัวเก็บประจุ (C) เมื่ออยู่ในวงจรไฟฟ้ากระแสสลับ ที่ มีกระแสไฟฟ้า I และมีความต่างศักย์ Vจะมีสมบัติดังรูป

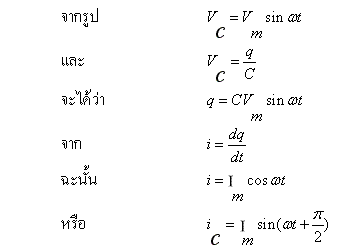
แสดงว่า กระแสไฟฟ้าในวงจรตัวเก็บประจุจะมีเฟสนำหน้าความต่างศักย์ไฟฟ้าของ ตัวเก็บ ประจุอยู่ 90 องศาในวงจรไฟฟ้ากระแสตรงกระแสจึง ผ่านไม่ได้ จึงถือว่ามีความต้านทานสูงมากแต่ในวงจรไฟฟ้ากระแสสลับ แม้ว่ากระแสจะผ่านไม่ได้ แต่จะมีการเหนี่ยวนำกลับไปกลับมาระหว่างแผ่นโลหะทั้งสองข้างทำให้คล้ายมีกระแสผ่านได้ แต่ตัวของมันจะมีสมบัติต้านการไหลของกระแสไฟฟ้าจึงคล้ายมีความ ต้านทาน ซึ่งเรียกว่า “ความต้านทานเชิงความจุ” (XC) มีหน่วยเป็นโอห์ม

3. วงจรขดลวดเหนี่ยวนำ (L) เมื่ออยู่ในวงจรไฟฟ้ากระแสสลับ ที่มีกระแสไฟฟ้า I และมีความต่างศักย์ Vจะมีสมบัติดังรูป

แสดงว่า กระแสไฟฟ้าในวงจรตัวเหนี่ยวนำจะมีเฟสตามความต่างศักย์ไฟฟ้าของตัวเก็บประจุอยู่ 90 องศาในวงจรไฟฟ้ากระแสสลับ ตัวเหนี่ยวนำจะมีสมบัติต้านการไหลของกระแสไฟฟ้า จึงคล้ายมีความต้านทาน ซึ่งเรียกว่า “ ความต้านทานเชิงเหนี่ยวนำ” (XL ) มีหน่วยเป็นโอห์ม

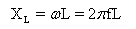
การเขียนแผนภาพเฟเซอร์

เป็นวิธีการที่จะช่วยในการรวมค่าความต่างศักย์ไฟฟ้าของวงจรไฟฟ้ากระแสสลับ โดยการเขียนลูกศรแทนความต่างศักย์ไฟฟ้าหรือกระแสไฟฟ้า ให้ความยาวของลูกศรแทนขนาดและตำแหน่งของลูกศรแสดงเฟสเริ่มต้นของปริมาณนั้น

โจทย์เรื่อง กฏการ เคลื่อนที่ของนิวตัน (Newton 's laws)

กฏการเคลื่อนที่ของนิวตัน (Newton 's laws )

กฏข้อที่ 1 ของนิวตัน

จากการเคลื่อนที่ของวัตถุ ต่างๆ ในชีวิตประจำวัน จะพบว่าวัตถุที่วางนิ่งอยู่บนพื้นราบเรียบจะ อยู่นิ่งต่อไปถ้าไม่ออกแรงกับวัตถุนั้น เช่น ก้อน หินที่วางบนพื้น เฉยๆ และวัตถุที่เคลื่อนที่ด้วยความเร็วคงที่ถ้าไม่มีการออกแรงกับวัตถุนั้น หรือออกแรง 2 แรง กับวัตถุนั้นในแรงที่เท่ากัน และทิศตรงข้ามกัน แล้ว วัตถุจะยังเคลื่อนที่ด้วยความเร็วคงที่เท่าเดิม เช่น เมื่อเรา อยู่ในรถ แล้วรถเกิดเบรกกระทันหัน ทำให้รถหยุดนิ่ง อย่างรวดเร็ว นันคือ มีแรง จากการเคลื่อนที่ไปข้างหน้า และแรงเสียดทานในการเบรกในทิศตรงข้ามกันแต่ ตัว เรายังเคลื่อนที่ไปข้างหน้าแม้รถจะหยุดแล้วก็ตาม กฎข้อที่ 1 ของนิวตัน เรียกอีกอย่างได้ว่า กฎความเฉื่อย

กฏข้อที่ 2 ของนิวตัน

จากการเคลื่อนที่ของวัตถุต่างๆ ในชีวิตประจำวัน จะพบว่า วัตถุที่เคลื่อนที่ด้วยความเร็วคงที่ เมื่อ เราออกแรงผลัก หรือ ดึงวัตถุที่เคลื่อน ที่อยู่นั้น ความเร็วจะเพิ่มขึ้นหรือลดลงได้ ซึ่งเรียกว่า วัตถุมี ความเร่ง เช่น เมื่อเราขับรถอยู่ แล้วเหยียบคันเร่งให้รถวิงเร็วขึ้น ความเร็วที่เพิ่มขึ้น เกิดจากแรงของรถ ที่เรียกว่า ความเร่งนั้นเอง และขนาดของความเร่งนั้นจะขึ้นอยู่กับน้ำหนักของวัตถุนั้นด้วย

โดยถ้า น้ำหนัก ของวัตถุ 2 วัตถุ เท่ากัน แต่ออกแรงให้วัตถุแต่ละวัตถุไม่เท่ากัน วัตถุที่ถูกออกแรงมากกว่าจะมีความเร่งมากกว่า และ ถ้าออกแรงให้กับ วัตถุ 2 วัตถุเท่ากัน ในขณะที่น้ำหนักทั้ง 2 วัตถุ ไม่เท่ากัน วัตถุที่น้ำหนักมากกว่าจะมีความ เร่งน้อยกว่า วัตถุที่มีน้ำหนักน้อยกว่า วัตถุ ที่เคลื่อนที่ตกจากที่สูง จะเคลื่อนที่ด้วยความร่งคงตัว แสดงว่า วัตถุนั้น ต้องมีแรงกระทำอยู่ จึงทำให้วัตถุเคลื่อนที่ด้วยความเร่ง แรงที่ทำกับ วัตถุนั้น เราเรียกว่า แรงดึงดูดของโลก หรือ แรงโน้มถ่วงของโลก และอาจเรียกได้อีก อย่างว่า น้ำหนักของวัตถุ

กฏข้อที่ 3 ของนิวตัน

ในชีวิตประจำวัน เราพบว่า เมื่อออก แรงกระทำกับวัตถุหนึ่ง วัตถุนั้นจะออกแรงตอบโต้กับ แรงที่เรากระทำในทันที เช่น เราสวมรองเท้าสเก็ตแล้วหันหน้าเข้ากำแพง เมื่อเราออกแรงพลักกำแพง ตัวเราจะเคลื่อนที่ออกจาก กำแพง นั้นแสองว่า กำแพงต้องมีแรงกระทำต่อเราด้วย จากตัวอย่างนี้ เรา เรียกแรงที่ เรากระทำต่อกำแพงว่า แรงกิริยา และเรียกแรงที่ กำแพงกระทำต่อเราว่า แรงปฏิกิริยา แรงทั้ง 2 นี้เรียกรวมกัน ว่า แรง คู่กิริยา - ปฏิกิริยา หรือ action - reaction pairs

แรงคู่กิริยา – ปฏิกิริยาที่กระทำระหว่างคนและโลก เมื่อคนยืนอยู่บนผิวโลก

จากรูปสามารถสรุปได้ว่า

1. แรงกิริยาและแรงปฏิกิริยาจะเกิดพร้อมกันเสมอ
2. แรงคู่กิริยา – ปฏิกิริยาเป็นแรงที่กระทำต่อวัตถุคนละวัตถุกัน ดังนั้นแรงคู่นี้จึงรวมกันไม่ได้
3. แรงคู่กิริยา - ปฏิกิริยาเกิดขึ้นได้ทั้งกรณีที่วัตถุสัมผัสกันหรือไม่สัมผัสกันก็ได้